Comparação de duas frações
(1) Por redução ao mesmo denominador
Se duas frações possuem denominadores iguais, a maior fração é a que possui maior numerador. Por exemplo:
| 3 5 | < | 4 5 |
|---|
(2) Tanto os numeradores como os denominadores das duas frações são diferentes
Devemos reduzir ambas as frações a um denominador comum e o processo depende do cálculo do Mínimo Múltiplo Comum entre os dois denominadores e este será o denominador comum às duas frações. Na seqüência, divide-se o denominador comum pelo denominador de cada fração e multiplica-se o resultado obtido pelo respectivo numerador.
Exemplo: Vamos comparar as frações 2/3 e 3/5. Como os denominadores são 3 e 5, temos que MMC(3,5)=15. Reduzindo ambas as frações ao mesmo denominador comum 15, aplica-se a regra de dividir o denominador comum pelo denominador de cada fração e na seqüência multiplica-se esse respectivo número pelo numerador.
| 2 3 | ? | 3 5 |
|---|
Multiplicando os termos da primeira fração por 5 e multiplicando os termos da segunda fração por 3, obteremos:
| 2 3 | = | 2×5 3×5 | ? | 3×3 5×3 | = | 3 5 |
|---|
Temos então os mesmos denominadores, logo:
| 2 3 | = | 10 15 | ? | 9 15 | = | 3 5 |
|---|
e podemos garantir que
| 2 3 | = | 10 15 | > | 9 15 | = | 3 5 |
|---|
(3) As frações possuem um mesmo numerador
Se os numeradores de duas frações forem iguais, será maior a fração cujo denominador for menor.
Exemplo: Uma representação gráfica para a desigualdade
| 3 4 | > | 3 8 |
|---|
pode ser dada geometricamente por:
3/4=6/8
| 3/8
|
|---|
Observe que a área amarelada é maior na primeira figura.
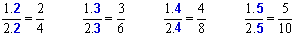
Frações equivalentes são frações que visivelmente são diferentes, mas se fizermos as devidas representações percebemos que representam a mesma quantidade. Veja o exemplo abaixo:
Imagine 4 circunferências, que fração pintada dessa circunferência será maior,
ou 
?
Se dividirmos essa circunferência ao meio e pintarmos 1 pedaço a fração que irá representar a parte pintada é
.
Se dividirmos essa circunferência em quatro partes e pintarmos 2 pedaços a fração que irá representar a parte pintada é.
Se dividirmos essa circunferência em 8 partes iguais e pintarmos 4 pedaços a fração que irá representar a parte pintada é.
Se dividirmos essa circunferência em 16 partes iguais e pintarmos 8 pedaços a fração que irá representar a parte pintada é
.
Todas as circunferências acima são iguais, mas cada uma está repartida em partes diferentes. As partes pintadas de cada circunferência representam a metade da circunferência, então as frações, , , representam a mesma quantidade da circunferência.
Essas frações são chamadas de frações equivalentes por indicarem a mesma quantidade.
Portanto, podemos dizer que
.
Para descobrir se uma fração é equivalente à outra existe um processo prático, veja:
Dizemos que é equivalente a , pois se multiplicamos tanto o numerador 1 por 2 como o denominador 2 por 2 iremos obter na outra fração 2 como numerador e 4 como denominador.
Portanto, uma fração será equivalente a outra se dividir ou multiplicar o numerador e o denominador de uma delas e chegar ao valor do numerador e do denominador da outra fração.
As frações são equivalentes.jpg)
, pois
3 x 2 = 6
4 x 2 8
3 x 3 = 9
4 x 3 12
3 x 4 = 12
4 x 4 16
Então, a propriedade da fração equivalente é:
Multiplicando ou dividindo o denominador e o numerador de uma fração pelo mesmo número chegaremos a uma fração equivalente a outra.
Frações equivalentes
Frações equivalentes são frações que representam a mesma parte do todo.
Exemplo: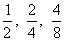 
são equivalentes
são equivalentes Para encontrar frações equivalentes devemos multiplicar o numerador e o denominador por um mesmo número natural, diferente de zero.
Exemplo: obter frações equivalentes à fração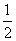 
.
. Portanto as frações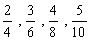 
são algumas das frações equivalentes a .
são algumas das frações equivalentes a 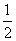.Simplificação de frações
Uma fração equivalente a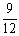 
, com termos menores, é 
. A fração foi obtida dividindo-se ambos os termos da fração pelo fator comum 3. Dizemos que a fração é uma fração simplificada de .
, com termos menores, é 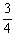. A fração 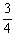foi obtida dividindo-se ambos os termos da fração 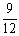pelo fator comum 3. Dizemos que a fração 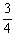é uma fração simplificada de 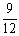. A fração 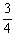não pode ser simplificada, por isso é chamada de fração irredutível. A fração não pode ser simplificada porque 3 e 4 não possuem nenhum fator comum
não pode ser simplificada, por isso é chamada de fração irredutível. A fração 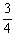não pode ser simplificada porque 3 e 4 não possuem nenhum fator comumImagine 4 circunferências, que fração pintada dessa circunferência será maior,
ou ?Se dividirmos essa circunferência ao meio e pintarmos 1 pedaço a fração que irá representar a parte pintada é
.Se dividirmos essa circunferência em quatro partes e pintarmos 2 pedaços a fração que irá representar a parte pintada é
.Se dividirmos essa circunferência em 8 partes iguais e pintarmos 4 pedaços a fração que irá representar a parte pintada é
.Se dividirmos essa circunferência em 16 partes iguais e pintarmos 8 pedaços a fração que irá representar a parte pintada é
.Todas as circunferências acima são iguais, mas cada uma está repartida em partes diferentes. As partes pintadas de cada circunferência representam a metade da circunferência, então as frações
, , , representam a mesma quantidade da circunferência.Essas frações são chamadas de frações equivalentes por indicarem a mesma quantidade.
Portanto, podemos dizer que
.Para descobrir se uma fração é equivalente à outra existe um processo prático, veja:
Dizemos que
é equivalente a , pois se multiplicamos tanto o numerador 1 por 2 como o denominador 2 por 2 iremos obter na outra fração 2 como numerador e 4 como denominador.Portanto, uma fração será equivalente a outra se dividir ou multiplicar o numerador e o denominador de uma delas e chegar ao valor do numerador e do denominador da outra fração.
As frações são equivalentes
, pois3 x 2 = 6
4 x 2 8
3 x 3 = 9
4 x 3 12
3 x 4 = 12
4 x 4 16
Então, a propriedade da fração equivalente é:
Multiplicando ou dividindo o denominador e o numerador de uma fração pelo mesmo número chegaremos a uma fração equivalente a outra.
