Sistemas de numeração
Há milhares de anos o modo de vida era muito diferente do atual. Os homens primitivos não tinham necessidade de contar. Eles não compravam, não vendiam, portanto não usavam dinheiro.
Com o passar dos anos, os costumes foram mudando e o homem passou a cultivar a terra, a criar animais, a construir casas e a comercializar. Com isso, surgiu a necessidade de contar.
Ávida foi tornando-se cada vez mais complexa. Surgiram as primeiras aldeias que, lentamente, foram crescendo, tornado-se cidades. Algumas cidades se desenvolveram, dando origem às grandes civilizações. Com o progresso e o alto grau de organização das antigas civilizações, a necessidade de aprimorar os processos de contagem e seus registros tornou-se fundamental.
Foram criados, então, símbolos e regras originando assim os diferentes
sistemas de numeração.
Sistema de numeração egípcio
Números representados pela simbologia
O sistema de numeração egípcio é muito diferente do implantados nos países ocidentais, que utiliza o modo arábico. Os números egípcios representam bem a cultura do povo que o criou, pois são verdadeiros símbolos dentro da matemática. O sistema é muito complicado para os ocidentes, mas para os egípcios, certamente é algo cultural, já enraizado e que só facilita a vida deles.
O sistema de numeração romano
Diversas civilizações da Antigüidade, além da egípcia, desenvolveram seus próprios sistemas de numeração. Alguns deles deixaram vestígios, apesar de terem sido abandonados. Assim, por exemplo, na contagem do tempo, agrupamos de 60 em 60; sessenta segundos compõem um minuto e sessenta minutos compõem uma hora. Isto é conseqüência da numeração desenvolvida na Mesopotâmia, há mais de 4000 anos. Lá era usada a base sessenta. Outro vestígio de uma numeração antiga pode ser observado nos mostradores de relógios, na indicação de datas e de capítulos de livros: são os símbolos de numeração romana. 
Estes são os símbolos usados no sistema de numeração romano:
| I | V | X | L | C | D | M |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
sistema de numeração indo-arábico
Os hindus, que viviam no vale do Rio Indo, onde hoje é o Paquistão, conseguiram desenvolver um sistema de numeração que reunia as diferentes características dos antigos sistemas: egípicio, babilônico e romano. Tratava-se de um sistema posicional decimal.
- Posicional: um mesmo símbolo representava valores diferentes, dependendo da posição ocupada.
- Decimal: porque eram feitos agrupamentos de dez em dez.
Por terem sido os árabes os responsáveis pela divulgação desse sistema, ele ficou conhecido como sistema de numeração indo-arábico.
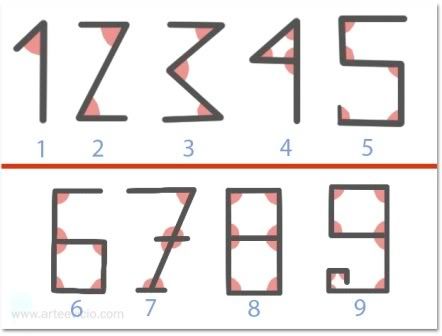
Agora, você sabia que a origem da forma dos números que utilizamos hoje se deve a quantidade de ângulos? Observe:
Com o tempo o sistema se popularizou e já não importava os ângulos para indicar quantidade, mas apenas o desenho bastava. O ocidente então adotou os números góticos que utilizamos hoje em dia, mais arredondados.
![x \cdot y = \begin{matrix} \underbrace{y+y+\cdots+y}\\{x}\\[-4ex] \end{matrix}](http://upload.wikimedia.org/math/f/5/a/f5a50bc2e418f83b2798e260770aa8f0.png)
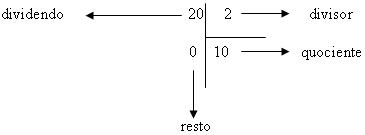
é o minuendo, 
é o subtraendo e 
é a diferença ou resto.
